Il testo che segue è tratto dal volume Prospettiva, edito da Hoepli, pg. 173 e segg.
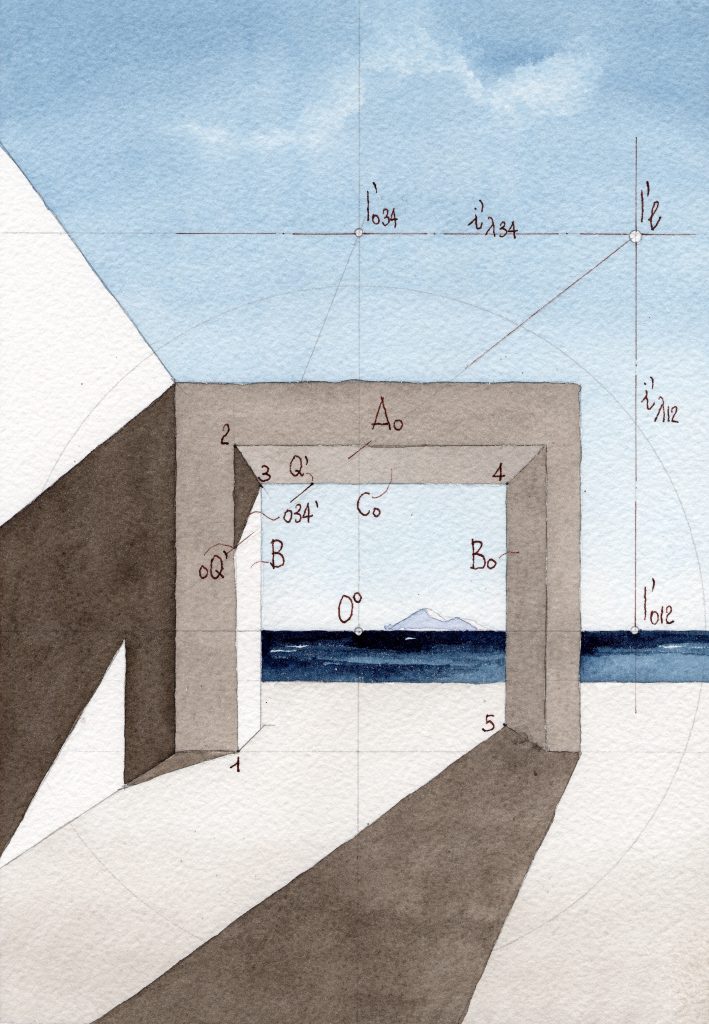
Consideriamo, per esempio, il portale della figura 11.12, ove il Sole è collocato davanti all’osservatore. Qui la faccia anteriore Ao è in ombra, mentre il fianco B dell’imbotte è in luce e la superficie inferiore dell’architrave, Co, nuovamente
in ombra. Dunque la separatrice d’ombra propria è così composta:
– dal tratto da 1 a 2, che separa Ao da B;
– dal tratto da 3 a 4, che separa Co da A e non è contiguo al tratto precedente;
– dal tratto da 4 a 5, che separa Bo da A.
La spezzata separatrice d’ombra propria comprende poi gli spigoli del telaio a contatto del terreno e i due spigoli verticali opposti a da 1 a 2 e da 4 a 5. Vediamo, allora, come si costruisce l’ombra in questo caso (figura 11.12):
- l’ombra del tratto verticale da 1 a 2 è portata sul geometrale e ha fuga nel punto I′o12 in cui la fuga del piano di luce i′λ12 taglia l’orizzonte; sul muro, è parallela a 1 − 2;
- l’ombra del tratto orizzontale da 3 a 4 è portata tanto sul geometrale, ove è parallela al tratto stesso, quanto sulla faccia B; qui l’ombra ha fuga nel punto I′
o34 in cui la fuga i′λ34 taglia la fuga del piano B, che è la retta verticale per passa per il punto principale; - questa ombra o34 incontra lo spigolo da 1 a 2 nel punto oQ: se si disegna il raggio di luce che passa per oQ si ha modo di determinare il punto Q del tratto da 3 a 4 che separa il segmento che porta ombra sulla faccia B dal segmento che porta ombra sul geometrale.
Appare, dunque, evidente come la spezzata separatrice d’ombra propria sia discontinua e come questa discontinuità sia, in qualche modo, risarcita dal segmento QoQ del raggio di luce che passa per questi due punti. La spezzata separatrice d’ombra propria di un solido può essere determinata anche per via geometrica, ma il modo più semplice e diretto consiste nel confrontare la direzione della luce con la giacitura dei piani rappresentati, ricostruendo nello spazio le relative entità proiettanti, rette e piani.