Come tutti i libri anche questo contiene alcuni capitoli nascosti.
Molti riguardano il passato: il flusso degli studi e delle invenzioni (nel senso del latino invenio) che hanno portato a ciò che qui è scritto e disegnato.
Altri capitoli non si vedono perché debbono ancora essere scritti, ma non è detto che saranno scritti da me o da un altro degli autori di questo libro.
Uno di questi ultimi capitoli si intitola “Lo spazio prospettico”.
Lo spazio prospettico è soggettivo e mutevole, ma c’è un modo per studiarne la forma.
Immaginiamo una scenografia tridimensionale (cioè una prospettiva solida) che sia stata costruita per creare una illusione perfetta nell’osservatore O, collocato nel centro di proiezione. Ebbene, è palese che mentre O non potrà distinguere la forma reale di ciò che vede e crederà di osservare uno spazio “normale”, lo spettatore S collocato lontano dal centro di proiezione potrà scorgere la vera forma e ne vedrà la tipica struttura piramidale.
Lo studio dello spazio spazio prospettico è l’analisi di questa struttura.
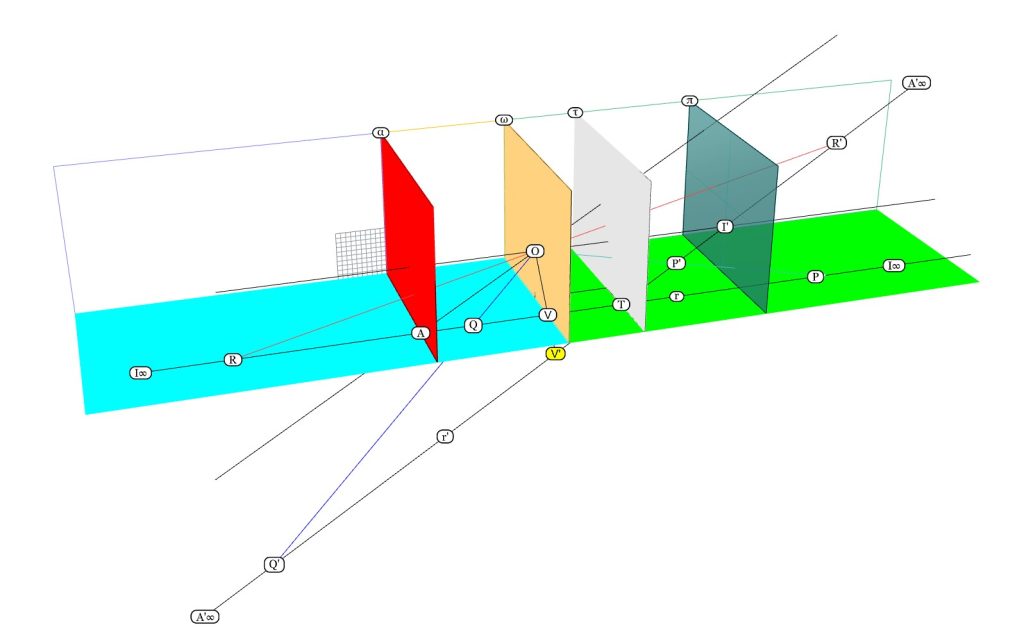
Consideriamo la macchina prospettica raffigurata qui sopra (il modello 3dm si può scaricare qui).
Questa macchina mette in relazione lo spazio euclideo, cioè il mondo come è, con lo spazio prospettico di O, cioè il mondo come a lui appare.
La macchina è costituita dal centro di proiezione O e da quattro piani:
– il piano delle fughe π;
– il piano delle tracce τ;
– il piano anteriore ω;
– il piano limite α.
La distanza tra i piani τ e π è uguale alla distanza tra i piani ω e α e possiamo immaginare che traslando π fino a farlo coincidere con τ e, simmetricamente, traslando α fino a farlo coincidere con ω la macchina della prospettiva solida
collassi in quella della prospettiva piana tradizionale, come caso particolare.
Consideriamo ora una qualsiasi retta r dello spazio euclideo e stacchiamo su di essa tre punti notevoli:
– il punto I∞ posto a distanza indeterminata davanti all’osservatore, cioè la direzione della retta r;
– il punto T nel quale r incontra il piano delle tracce τ;
– il punto A nel quale r incontra il piano limite α;
– il punto I∞ posto a distanza indeterminata dietro all’osservatore, cioè ancora la direzione della retta r;
Infatti, un punto a distanza indeterminata come I∞ deve intendersi il medesimo sia che si percorra la retta in un senso, per esempio avanti all’osservatore, sia che la si percorra in senso opposto e per questa ragione si identifica con la direzione della retta.
Costruiamo ora le rette proiettanti OI∞ e OA per osservare quanto segue:
– la retta proiettante OI∞ interseca il piano delle fughe π nel punto I′ che è la fuga della prospettiva solida della retta r;
– la retta r incontra il piano delle tracce τ nel punto T che è la sua traccia;
– la prospettiva solida r′ della retta r è dunque la retta TI′, che, osservata da O
si confonde con la retta r dello spazio euclideo;
– la retta proiettante OA è parallela a r′ perché i piani τ e π e i piani ω e α sono, a
coppie, equidistanti e i segmenti AT e OI′ sono uguali e paralleli;
– dunque la retta OA incontra la retta r′ nel punto A′∞ che è a distanza indeterminata ed è la direzione delle due rette r′ e OA.
Tra i punti della retta r dello spazio euclideo e i punti della retta r′ dello spazio prospettico intercede ora una corrispondenza biunivoca, infatti, dato un qualsiasi punto P di r nello spazio euclideo, esiste nello spazio prospettico un solo punto P′ di r′ che gli corrisponde e viceversa, dato un qualsiasi punto P′ di r′ esiste nello spazio euclideo un solo punto P di r che gli corrisponde.
Lo spazio prospettico si divide in due zone: lo spazio anteriore (in verde nella figura) e lo spazio posteriore (in azzurro nella figura).
Il confine tra i due semispazi è il piano anteriore ω (in giallo nella figura).
Ovviamente, in questo schema, bisogna immaginare i colori estesi all’intero semispazio delimitato dal piano omega a sua volta indefinitamente
esteso.
Nel semispazio verde si proiettano i punti P del semispazio euclideo anteriore che è compreso tra l’infinito anteriore e il piano anteriore ω; nonché i punti Q del semispazio euclideo posteriore che è compreso tra il piano limite (in rosso nella figura) e l’infinito posteriore.
Si noti che questi punti Q generano una prospettiva rovesciata.
Nel semispazio azzurro si proiettano i punti compresi tra il piano anteriore ω (in giallo) e il piano limite α (in rosso).
Dunque si verifica questa anomalia: il semispazio verde sostiene la prospettiva dritta o rovesciata di tutto lo spazio euclideo, tranne la porzione compresa tra i piani rosso e giallo, che si proietta nel semispazio azzurro.
Questa parte dello spazio euclideo, compresa tra i piani rosso e giallo, si potrebbe chiamare “spazio di Ames”, perché le figure tridimensionali che si trovano in questo spazio hanno prospettive solide caratterizzate dalle forme e dagli effetti percettivi della nota camera distorta detta anche camera di Ames. In particolare, la camera distorta è una prospettiva solida d’angolo collocata nello spazio di Ames.
Le formule per la costruzione di uno spazio scenografico, che si trovano nei capitoli 17 e 18 (rispettivamente a pag. 311 e pag. 329 e seguenti) permettono anche si generare lo spazio di Ames, come quello delle figure 17.20 e 17.21.
